



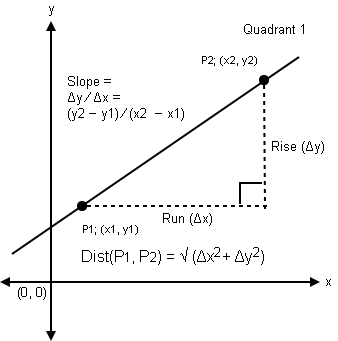
Distance Formula


The Distance Formula provides a method to determine the length of a line segment that is sloped, horizontal or vertical.
The Distance Formula is given as:
Dist(P1, P2) = √(Δx2 + Δy2)
“Dist” is an abbreviation for the word distance. P1 and P2 are each unique points on the same line segment. Δx is a horizontal distance and Δy is a vertical distance:
P1 = (x1, y1)
P2 = (x2, y2)
(P1 and P2 are Cartesian Coordinates)
Δx = Run = x2 − x1
Δy = Rise = y2 − y1
(Δx and Δy have same definition as Linear Equation Formula where y = mx + b, the slope m = Rise / Run or m = Δy / Δx)
Please refer to the Cartesian coordinate image (right) that illustrates P1, P2, Δx and Δy on a sloped line segment.
Geometric visual examination of Distance Formula:
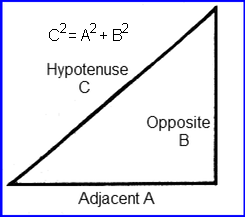
For a right triangle hypotenuse length the Distance Formula equates to the Pythagoras Formula…
(Pythagorean Theorem is the math and geometry that proves Pythagoras Formula)
Pythagoras Formula:
C2 = A2 + B2
C = √( A2 + B2)
where,
A = Δx = x2 − x1
B = Δy = y2 − y1
We can now see that:
C2 = A2 + B2 = Δx2 + Δy2
C2 = A2 + B2 = (x2 − x1)2 + (y2 − y1)2
C2 = A2 + B2 = (x2 − x1)2 + (y2 − y1)2 = Dist(P1, P2)2
√C2 = √Dist(P1, P2)2
C = Dist(P1, P2)
Geometric visual of Pythagoras Formula:
We can now conclude:
Pythagoras Formula = Distance Formula
Distance Formula problems exampled:
Dist(P1, P2) = √((x2 − x1)2 + (y2 − y1)2)
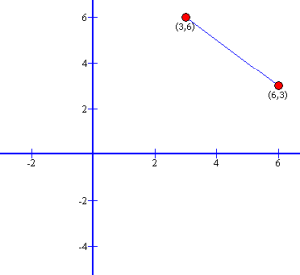
Given the coordinates,
P1 = (6, 3)
P2 = (3, 6)
The distance between P1 and P2 is,
Δx = x2 − x1 = 3 − 6 = −3
Δy = y2 − y1 = 6 − 3 = 3
Dist(P1, P2) = √(−32 + 32) = √18 = 3√2
P1 = (6,3), P2 = (3, 6):
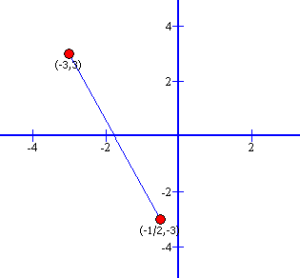
Given the coordinates,
P1 = (−3, 3)
P2 = (−1/2, −3)
The distance between P1 and P2 is,
Δx = x2 − x1 = −1/2 − (−3) = −1/2 + 3 = 2 1/2
Δy = y2 − y1 = −3 − 3 = −6
Dist(P1, P2) = √((2 1/2)2 + (−6)2) = 6 1/2
P1 = (−3, 3), P2 = (−1/2, −3):
 Top of Page
Top of PageCopyright © DigitMath.com
All Rights Reserved.