



Math Fractions
Reducing-Equivalent-Mixed-Complex


Fractions are a portion of something. If we peel an orange it has 8 slices. Each slice is a fractional proportion of the whole orange. Each equal slice is 1/8th (1 divided by 8) of the orange or one of eight slices.
A fraction is something smaller than a whole. In math they represent division. A piece of cake, slice of pie or pizza are each a portion of something larger.
Solving fractions we sometimes use addition, subtraction and multiplication.
Simple fraction notation is a horizontal line with an integer number above and an integer number below:
M
N
M is divided by N. M is the numerator. N is the denominator. For now M and N will be integers. A denominator cannot equal zero.

Slice of the orange is one of eight equal portions.
Equivalent Fractions
Equivalent fractions are two or more fractions that look different from each other, but are the same value. They are sometimes called like fractions or stated as equivalent ratios.
Ordering fractions helps us see they are equivalent value and of equal portion:
32/64 = 16/32 = 8/16 = 4/8 = 2/4 = 1/2 is something divided into 2 equal portions.
16/64 = 8/32 = 4/16 = 2/8 = 1/4 is something divided into 4 equal portions.
8/64 = 4/32 = 2/16 = 1/8 is something divided into 8 equal portions.
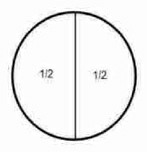
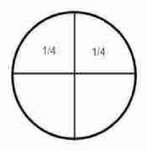
Fraction Circles
Each fraction is using a multiple of 2. Multiplying the numerator and denominator of a fraction by the same number is always an equivalent fraction. Dividing the numerator and denominator of a fraction by the same number is always an equivalent fraction and is for reducing fractions. The most efficient fraction reducer is when the greatest common divisor of the denominator is the numerator, the resulting numerator is always 1.
Comparing fractions helps us see the value one fraction has to another:
1/8 < 1/4 < 1/2 < 1/1 and 1/1 = 1
1/8 × 8 = 1/8 × 8/1 = 1
2/8 and 1/4 are equivalent, 1/8 is half the size of 1/4.
4/8 and 1/2 are equivalent, 1/8 is quarter the size of 1/2.
8/8 and 1 are equivalent, 1/8 is eighth the size of 1.
1/4 × 4 = 1/4 × 4/1 = 1
2/4 and 1/2 are equivalent, 1/4 is half the size of 1/2.
4/4 and 1 are equivalent, 1/4 is quarter the size of 1.
1/2 × 2 = 1/2 × 2/1 = 1
2/2 and 1 are equivalent, 1/2 is half the size of 1.
Reducing Fractions
Whenever possible we want to simplify fractions. It is reducing fractions to their simplest form. A lot of solving math problems is applying rules so that an answer or result of an operation is easiest to work with.
When the numerator is smaller than the denominator we have a proper fraction.
When the numerator is larger than the denominator we have an improper fraction that should be reduced to a mixed fraction.
4
5
Proper Fraction
5
4
Improper Fraction
Mixed Fractions
Mixed fractions are a combination of integers and fractions. 1 2/3 and 3 1/2 are mixed fractions.
To simplify the improper fraction 5/3:
First, break the improper fraction into a math form we easily understand:
5/3 = 1/3 + 1/3 + 1/3 + 1/3 + 1/3
Add the 1’s in the numerator. Every time they add up to the value of the denominator place a parenthesis around them:
(1/3 + 1/3 + 1/3) + 1/3 + 1/3
Next, add the groups of parenthesis:
1 + 1/3 + 1/3
Write the answer by adding the remaining values together:
1 + (1/3 + 1/3) = 1 2/3
To simplify the improper fraction 7/2:
7/2 = 1/2 + 1/2 + 1/2 + 1/2 + 1/2 + 1/2 + 1/2 =
(1/2 + 1/2) + (1/2 + 1/2) + (1/2 +1/2) + 1/2 =
3 + 1/2 =
3 1/2
To simplify the improper fraction 9/4:
9/4 =
(1/4 + 1/4 + 1/4 + 1/4) + (1/4 + 1/4 + 1/4 + 1/4) + 1/4 =
2 + 1/4 =
2 1/4
Complex Fractions
A fraction that is divided by a fraction is a complex fraction. Since fractions are math division they are often different quantities of ingredient portions that combine to form or create something, and can be stated as ratios and proportions. The ingredients that are used to bake a cake are each different quantities of different food items that are combined. Each ingredient can be stated as a ratio or proportion of the entire cake or of another cake ingredient.
To solve complex fractions we rewrite the math problem to multiply the numerator fraction by the flipped over denominator fraction. By flipping a fraction over the numerator becomes the denominator and denominator becomes the numerator, the reciprocal of a fraction.
Simple fractions can be written as complex fractions to understand how complex fractions work. We’ll use the math rule that states any quantity divided by 1 is the same as the original quantity:
15/26 = (15/1) / (26/1) = (15/1) × (1/26) = 15/26
To reduce the complex fraction: (1/2) / (1/4):
Rewrite the fraction division as a multiplication problem.
(Reciprocal of a fraction: 1/4 is flipped over, it becomes 4/1)
(1/2) / (1/4) = (1/2) × (4/1) = 4/2
If the result is an improper fraction then reduce that fraction to obtain the answer.
4/2 = (1/2 + 1/2) + (1/2 + 1/2) = 2/2 + 2/2 = 1 + 1 = 2
Explanation - You have 1/2. The 1/2 is 1/4, a fourth, of some number. The total is 2 because 4 halves equal 2.
To simplify and reduce the complex fraction: (12/3) / (7/5):
(12/3) / (7/5) = (12/3) × (5/7) = 60/21 =
21/21 + 21/21 + 18/21 = 1 + 1 + 18/21 = 2 18/21
18 and 21 are both divisible by 3 and is the least common multiple of 18 and 21. 18/21 can be reduced:
2 18/21 = 2 6/7
Copyright © DigitMath.com
All Rights Reserved.
| Addition |
| Subtraction |
| Multiplication |
| Division |
| Prime Numbers |
| Decimals and Place Value |
| Square Root |
| Rational and Irrational Numbers |
| Multiplication Table |
| Adding Decimals |
| Subtracting Decimals |
| Multiplying Decimals |
| Square Numbers Conversion Tables |
| Factoring Polynomials |
| Factors and Factoring Defined |
| Prime Factorization |
| Algebraic Expressions and Math Terms |
| Important Algebraic Expressions |
| Difference of Squares |
| Factoring Trinomials |
| Factoring by Grouping |
| Cube-Formula(s) |
| Graphing Linear Equations |
| Linear Equations In Two Variables |
| System of Equations |
| Linear Function |
| Distance Formula |
| Midpoint Formula |
| Absolute Value |
| Polynomial Long Division |
| Synthetic Division |
| Radicals Adding Subtracting |
| Radical Expressions |
| Simplifying Radical Expressions |
| Factoring Quadratic Equations |
| Factoring by Completing the Square |
| Quadratic Equation Formula |
| Common Logarithm Tables |
| Logarithms Definition |
| Logarithm Properties |
| Common Logarithms |
| Antilogs |
| Natural Logarithms |
| Sequence Convergence & Divergence |
| Summation Notation |
| Factorials |
| Factorials for Binomial Expansion |
| Pascals Triangle |
| Mathematical Induction |
| What are Parallelograms? |
| Parallelogram Area |
| Perimeter of a Parallelogram |
| What is a Quadrilateral? |
| 3×3 Matrix Determinant |
| 4×4 Matrix Determinant |
| 3×3 Cramer’s Rule |
| Circle |
| Ellipse |
| Parabola |
| Hyperbola |
| Trigonometric Functions Table |
| Radians |
| Sine Graph |
| Cosine Graph |
| Tangent Graph |
| Using Trigonometric Functions Table |
| Babylonian/Pythagorean/Egyptian |
| Greek Mathematics |
| Chinese Indian Islamic Math |
| Medieval European Renaissance Math |
| Scientific Revolution Math |
| Modern Math |
| Twentieth Century Math |
