Logarithms
Defined and Explained

Logarithms have important use and application in Physics, Chemistry, Biology and Economics, as well as Advanced Mathematics. To most easily understand Logarithms it is suggested to first completely understand Math Exponents.

Definition of Logarithms

Logarithms equate to Exponents, when we say:

bm = x

b is the base, m is the exponent and x is the mth power of b.

Let b and x be positive numbers with b not equal 1. If bm = x then m is called the Logarithm of x to the base b:

logb x = m when bm = x

Example:

log2 8 = 3 when 23 = 8

Base

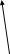
Power

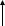
Exponent

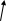
Base

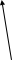
Exponent

Power

The Logarithm Notation is, from left to right, base-power-exponent while Exponent Notation is base-exponent-power.

Here are some examples of how Logarithms equate to Exponents:

log10 10,000 = 4 is the same as 104 = 10,000

log10 .01 = −2 is the same as 10−2 = .01

(because 10−2 = 1/102 = 1/100 = .01)

log16 1/4 = −1/2 is the same as 16−½ = 1/16½ = 1/4

log½ 8 = −3 is the same as (1/2)−3 = 1/(1/2)3 = 1/(1/8) = 8

42 = 16 is the same as log4 16 = 2

4−3 = 1/64 is the same as log4 1/64 = −3

40 = 1 is the same as log4 1 = 0

32 = 9 is the same as log3 9 = 2

3−2 = 1/9 is the same as log3 1/9 = −2

Properties of Logarithms

Since Logarithms equate to Exponents it is easiest to understand the three properties of Logarithms in terms of the rules of Exponents.

Property 1:

The log of a product is the sum of the logs.

logb x1x2 = logb x1 + logb x2 is the same as bm1bm2 = bm1 + m2

Example:

log2 (8)(4) = log2 8 + log2 4

Solve each logarithm by using the exponent equation bm = x.

log2 (8)(4) = m is the same as 2m = 32 when m = 5

log2 8 = m is the same as 2m = 8 when m = 3

log2 4 = m is the same as 2m = 4 when m = 2

Replace each logarithm with its value m:

5 = 3 + 2

Property  2:

The log of a quotient is the difference of the logs.

logb (x1/x2) = logb x1 − logb x2 is the same as (bm1/ bm2) = bm1 − m2

Example:

log5 (125/25) = m is the same as 5m = 5 when m = 1

log5 125 = m is the same as 5m = 125 when m = 3

log5 25 = m is the same as 5m = 25 when m = 2

Replace each logarithm with its value m:

1 = 3 − 2

Property  3:

The log of the rth power of x is r times the log of x.

logb xr = r logb x is the same as bmr = (bm)r

Example:

log10 1003 = 3 log10 100

log10 1003 = m is the same as 10m = 1,000,000 when m = 6

3 log10 100 = m is the same as (3) (10m = 100) when m = 2

Replace each logarithm with its value m:

6 = (3) × 2

Common Logarithms

All Logarithms to the base 10 are known as Common Logarithms and are typically written without a base value:

log 10 = m is the same as log10 10 = m

If the Logarithm is an integral power of 10 it is easy to solve by the Logarithm base-power-exponent and exponent base-exponent-power relationship defined above in the Definition of Logarithms. To solve these Common Logarithms requires that we find an exponent value that results in the base 10 raised to an exponent value that will equal a power of 10:

log10 100 = 2 because 102 = 100

log .0001 = log 10−4 because 10−4 = .0001

The common log of most positive numbers not an integral power of 10 are difficult to solve:

log 5 = m is the same as 10m = 5

log 1.26 = m is the same as 10m = 1.26

To solve a Common Logarithm that is not an integral power of 10 requires the use of a Log Table. A Log Table is a compilation, by advanced math methods, that indicates the approximate log of any number between 1 and 10. As you will see, the table enables every log to be approximated for every positive number.

Partial Log Table:

The values from the columns labeled by numbers 0 - 9 are the mantissa of a Logarithm.

We’ll use the Partial Log Table to solve:

log 1.26 = m

First look down the table column labeled x for the value 1.2. Next move horizontally across that row to the column labeled 6 (the 6 from 1.26). The value is .1004:

m = .1004 and the log 1.26 = .1004

To find the log of values greater than 10 the power of the Logarithm requires a conversion of the power so that it is a single whole number having 2 decimal positions:

log 542 = m

(Use Logarithm Property 1 to change the characteristic to a single whole number)

log 542 = log (5.42)(102) = log 5.42 + log 102 = m

(Log Table mantissa of 5.42 is .7340)

m = log 5.42 + log 102 = .7340 + 2 = 2.7340

Because of their base 10 Common Logarithms are often used for Logarithmic Scales. The Logarithmic Scale is a linear representation of something that is increasing (or decreasing) exponentially:

Antilogs

To find the Antilogarithm of a Common Logarithm is the reverse process of finding a log. The Antilog is simply 10m.

Formal math definition:

antilog m = x if log x = m

Let m be any real number.

Suppose you were asked to find the Antilog 2.6848:

The mantissa .6848 came from a Log Table. Skim through the table to locate this mantissa. You see the row 4.8 and the column 4 is where the mantissa .6848 is located. Thus the mantissa corresponds to 4.84 and you have determined the digits of the Antilog.

Partial Log Table:

antilog .6848 = 4.84

Now use the characteristic to place the decimal point. Because the characteristic is 2, multiply by 102. This means you move the decimal point 2 places to the right.

antilog 2.6848 = 484

102.6848 equals 483.949 and is approximately equal to 484

Natural Logarithms

In Calculus the Logarithmic Function of most importance is a Natural Logarithm. Its base is an irrational number, e, which is approximately equal to 2.71828 . Except for the base, e, Natural Logarithms look and are solved the same as other Logarithms.

loge x = m when em = x

ln x (ln x is the same as loge x, both show a Log Natural)

ln is an abbreviation from the Latin name Logarithmus Naturali.

Within the studies of natural sciences and economics many applications of ln and e exist. e is about how much growth, as a rate, occurs in a specified amount of time. Log Natural, ln, is about the time required to get to a rate of growth.

e4 is 54.5981. After 4 units of time we would have 54.5981 times the amount or quantity we began with.

ln 54.5981 is 4. A growth rate of 54.5981 would require 4 units of time.

An Exponential and a Logarithm are inverse math functions:

exp(ln x) = x

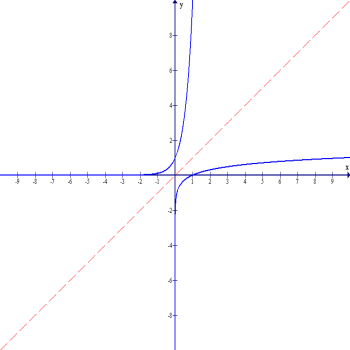
Exponential

Logarithmic

Copyright © DigitMath.com

All Rights Reserved.