Mobile Math Website

Linear Functions

The Linear Function provides a convenient method to determine behavior of a sloping straight line on a Cartesian Coordinate System before drawing a graph using rectangular coordinates. It is function math for a Linear Equation.

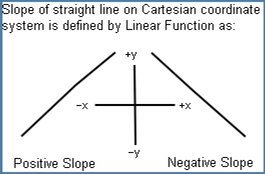
The Linear Function defines sloped straight lines as:

f(x) = ax + b and a ≠ 0, for all real numbers.

a is slope. b is the y intercept, the value of y when x = 0.

When a is:

1. > 0; the graph line is rising, a positive slope.
2. < 0; the graph line is falling, a negative slope.

When b is:

1. > 0; the graph line is above a Cartesian coordinate origin, (0, 0), when intersecting the y axis. When x = zero then y > zero.
2. < 0; the graph line is below a Cartesian coordinate origin when intersecting the y axis. When x = zero then y < zero.
3. = 0; the graph line passes through a Cartesian coordinate origin.

When b ≠ 0 there exists an x intercept when y = 0.

The Linear Function does not define:

1. A horizontal line; When a = 0, then f(x) = b, a constant. f(x) = c is the Constant Function.
2. A vertical line; Slope a would be infinite.

Linear Function Examples

f(x) = ax1 + b

g(x) = ax2 + b

h(x) = ax3 + b

Where x1 ≠ x2 ≠ x3

f(x), g(x) and h(x) are different points on the same line as unique (x, y) coordinates. Their a and b values of all linear functions are the same.

Let a = 2 and b = 3;

y intercept is value of b and graph coordinate (0, 3).

Replace f(x), g(x) and h(x) math functions by y, then for all values of x;

y = 0 = 2x + 3

2x = −3

x = −3/2

x intercept when y = 0 is: −1 ½

y = 0 = 2x + 3 then x = −3/2

f(x) = ax + b1

g(x) = ax + b2

Where b1 ≠ b2,

Lines f(x) and g(x) are parallel separated by the absolute value of any perpendicular between b1 and b2.

f(x) = a1x + b

g(x) = a2x + b

Where a1 ≠ a2,

Lines f(x) and g(x) intersect at exactly one point (0, b). It is the only value for x that provides the same y for both linear functions:

f(x) = g(x) when x = 0

f(x) = a1x + b

g(x) = a2x + b

Where a1 ≠ a2 and a2 < 0

Line f(x) has positive slope and line g(x) has negative slope. f(x) and g(x) intersect at exactly one point; (0, b). It is the only value for x that provides the same y for both functions:

f(x) = g(x) when x = 0

Linear Function Identity

When a = 1 and b = 0 then y = f(x) = ax

Its graph is a straight line passing through a Cartesian coordinate origin, bisecting at 45 degree right angles the first and third quadrants.

Copyright © DigitMath.com

All Rights Reserved.