Midpoint of a Line Segment and the Midpoint Formula

The midpoint of a line segment is the point M on the segment such that:

Dist(P1, M) = Dist(P2, M)

“Dist” is an abbreviation for distance. P1 is a point on a line segment and P2 is a different point on the same line segment. M is a point ½ the distance between P1 and P2, and represents an exact same distance from P1 or P2.

Similar to the Distance Formula, to understand the Midpoint Formula we must consider a horizontal line segment, a vertical line segment and a line segment that has slope, is neither horizontal or vertical.

P1 = (x1, y1)

P2 = (x2, y2)

(Both P1 and P2 are Cartesian Coordinates)

Δx = Run = x2 − x1

Δy = Rise = y2 − y1

(Same definition as Linear Equation Slope where y = mx + b and the slope m = Rise / Run or m = Δy / Δx)

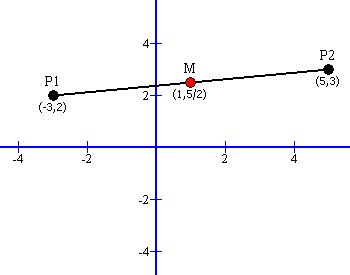
“To grasp the logic explaining the Midpoint Formula it is recommended to first understand the Distance Formula.”

Please review the Cartesian coordinate image (above right) that illustrates P1,and P2, on a sloped line segment.

Should y1 = y2, then y2 − y1 = 0, the line segment is horizontal with length x2 − x1:

M = ((x2 + x1) / 2, y1) where (x2 + x1) / 2 is the average of two x coordinate values.

Should x1 = x2, then x2 − x1 = 0, the line segment is vertical with length y2 − y1:

M = (x1, (y2 + y1) / 2) where (y2 + y1) / 2 is an average of the two y coordinate values.

For a sloped line the midpoint is ½ the distance between point P1 and point P2, and is given as the point defined by coordinates:

M = ((x2 + x1) / 2, (y2 + y1) / 2)

Copyright © DigitMath.com

All Rights Reserved.