System of Linear Equations (Simultaneous Equations)

A System of Equations is two or more Linear Equations whose straight lines intersect at an exact same point. The point of intersection is described by identical Cartesian Coordinates, (x, y).

Solving a System of Equations two equations are evaluated together simultaneously for a value x. Then each equation is solved individually using the x value to validate they assign the same y value of the coordinate.

The following examples demonstrate how to solve a System of Equations:

4x + 5y = 18 and x − 3y = −4

Isolate y to one side of each equation.

5y = 18 − 4x and x + 4 = 3y

(18 − 4x) / 5 = y and (x + 4) / 3 = y

(18 − 4x) / 5 = y = (x + 4) / 3

Solve both equations simultaneously for x.

(18 − 4x) / 5 = y = (x + 4) / 3

(18 − 4x) / 5 = (x + 4) / 3

3 (18 − 4x) = 5 (x + 4)

54 − 12x = 5x + 20

54 − 20 = 5x + 12x

34 = 17x

34/17 = x

2 = x

Check that each equation provides identical y using the same x value.

18 − 4 (2) = 5y

18 − 8 = 5y

10/5 = y

2 = y

x + 4 = 3y

2 + 4 = 3y

6/3 = y

2 = y

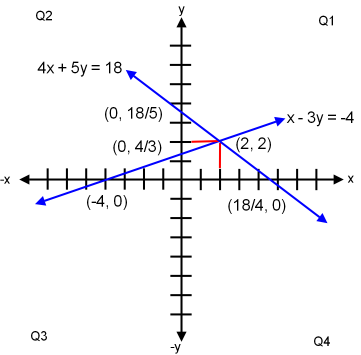
Graph of linear equations 4x + 5y = 18 and x − 3y = −4 showing intersect coordinate (2, 2).

The best way to graph each linear equation is by the x and y intercepts.

For 4x + 5y = 18:

x = 0 when y = 18/5

and x = 18/4 when y = 0

For x − 3y = −4:

x = 0 when y = 4/3

and x = −4 when y = 0

Lines intersect coordinate is (2, 2).

3x + 2y = 7 and 4x + 2y = 5

Isolate y to one side of each equation.

2y = 7 − 3x and 2y = 5 − 4x

7 − 3x = 2y = 5 − 4x

(7 − 3x) / 2 = y = (5 − 4x) / 2

Solve both equations simultaneously for x.

(7 − 3x) / 2 = y = (5 − 4x) / 2

7 − 5 = −4x + 3x

2 = −1x

−2 = x

Check that each equation provides identical y using the same x value.

7 − 3x = 2y

7 − 3 (−2) = 2y

7 + 6 = 2y

13/2 = y

5 − 4x = 2y

5 − 4 (−2) = 2y

5 + 8 = 2y

13/2 = y

Lines intersect at coordinate (−2, 13/2).

2x + 3y = 4 and x − 2y = 3

Isolate y to one side of each equation.

4 − 2x = 3y and x − 3 = 2y

(4 − 2x) / 3 = y and ( x − 3 ) / 2 = y

(4 − 2x) / 3 = y = (x − 3) / 2

2 (4 − 2x ) = y = 3 (x − 3)

Solve both equations simultaneously for x.

2 (4 − 2x ) = y = 3 (x − 3)

8 − 4x = 3x − 9

17 = 7x

17/7 = x

Check that each equation provides identical y using the same x value.

4 − 2 (17 / 7) = 3y

28 / 7 − 34 / 7 = 3y

−6/7 = 3y

−6/21 = y

−2/7 = y

x − 3 = 2y

17 / 7 − 3 = 2y

17 / 7 − 21 / 7 = 2y

−4/7 = 2y

−2/7 = y

Copyright © DigitMath.com

All Rights Reserved.