



Trigonometry


Trigonometry is the branch of mathematics that analyzes the relations between the sides and angles of triangles.
An angle is the union of two closed rays originating from the same point. The point where the rays intersect is the vertex and each ray is a side of the angle.
To identify an angle we often use points on their sides:
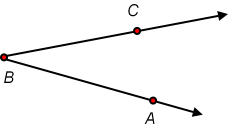


Angles are also often measured in degrees. There are 180° (180 degrees) in the triangles we will study. Each degree can be divided into 60 minutes if finer measurement is required.
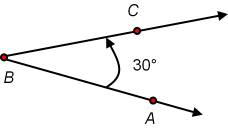
The angle can be identified by the vertex point only if this does not cause any confusion. Instead of angle ABC or angle CBA we can just write angle B:

B is 30°
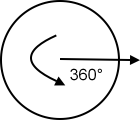
Normally angles measure between 0° and 360°. 360 is the number of degrees of a circle. A right angle measures 90°. An acute angle measures between 0° and 90°, an obtuse angle measures between 90° and 180°:

A is acute if 0° <

A < 90°

A is obtuse if 90° <

A < 180°
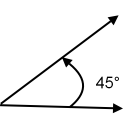

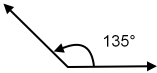
45° acute angle.
90° right angle.
135° obtuse angle.
Angle rotation that is increased from 0° to 360° completes a circle.
A triangle is a three sided closed figure on a plane surface. The vertex of a triangle is the same as the vertex for two intersecting rays. The addition of a third line that intersects both rays, but not at a vertex, creates a triangle; this line segment is the triangle opposite side. A line from the triangle vertex and drawn parallel the opposite side defines triangle altitude, h:
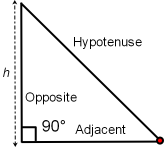
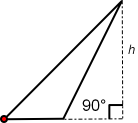
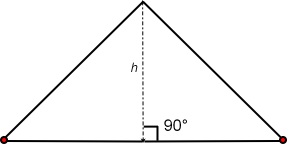
Of the three triangle images above, the first triangle image (left) is a right triangle that has two sides intersecting at 90°; one line is perpendicular the other line, these two lines form a right angle. The middle and third triangles do not have two sides that form a right angle. For these triangles a right angle must be drawn so that the altitude, h, can be visualized.
It is important to be able to recognize the right angle and altitude, h, of a triangle for the Pythagorean Theorem which states:
a2 + b2 = c2
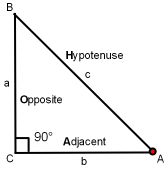
Where a is the length of the adjacent side, the opposite side length is b and the length of c is the hypotenuse. This math formula often helps us solve trigonometry problems.
Trigonometric Functions Sine, Cosine and Tangent:
The three most important trigonometric functions of an acute angle are the sine, cosine and tangent. These trig functions are ratios defined in terms of angle A:
Sine A = a / c
Think of: Opposite / Hypotenuse
Cosine A = b / c
Think of: Adjacent / Hypotenuse
Tangent A = a / b
Think of: Opposite / Adjacent
To remember these trig functions think:
SOH-CAH-TOA
… and sine, cosine and tangent are abbreviated as sin, cos and tan.
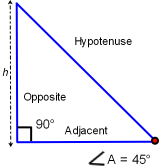
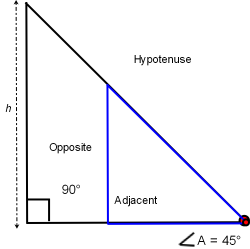
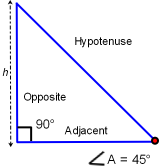
These trig functions show us that regardless of the lengths of the opposite, adjacent and hypotenuse sides; all right triangles with identical angle A degrees will create identical sin, cos and tan regardless of actual triangle size. It is a statement the triangles are congruent, similar triangles. If the opposite side length is increased then the adjacent and hypotenuse sides must increase to have identical angle A. If the hypotenuse length is decreased then the adjacent and opposite side lengths must also decrease for angle A to remain constant.
Two 45-45-90 triangles of different size have identical angles. Then both triangles have identical sine, cosine and tangent:
Isosceles and Equilateral Triangles (Special Triangles):
To find the trig functions of an acute angle a trigonometry table must be used. The exception is the trig functions for 30°, 45° and 60° angles that can be determined without a trig table. For this purpose we consider both isosceles and equilateral triangles.
An isosceles triangle has two sides of equal length with angles opposite the equal sides of equal measure. The equal angles each measure 45°. The isosceles triangle is therefore a 45° 45° 90° triangle. If we suppose that the lengths of the adjacent and opposite sides are both one, then by the Pythagorean Theorem:
c2 = 12 + 12 = 2
c = √2 = hypotenuse length
Thus, by SOH-CAH-TOA:
Sin 45° = O / H = 1 / √2 = (1 √2) / (√2 √2) = √2 / 2
Cos 45° = A / H = 1 / √2 = √2 / 2
Tan 45° = O / A = 1 / 1 = 1
45° 45° 90° isosceles triangle:
An equilateral triangle has three sides that are equal length and three angles that are equal measurement. A distinguishing feature is that each angle is 60°. Because the lengths of its sides are equal and the measures of its angles are equal the altitude (height) of an equilateral triangle bisects (cuts in half) any side at a perpendicular and its corresponding vertex. A line representing the altitude, h, separates the single equilateral triangle into two acute right triangles with each triangle having 30° 60° and 90° angles.
Bisecting the equilateral triangle creates two 30-60-90 triangles:
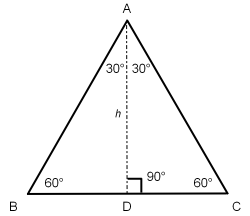
For a 30° 60° 90° triangle, from angle A, the hypotenuse length will be twice the length of the opposite side. By using the Pythagorean Theorem to solve for the adjacent length:
c2 = a2 + b2
22 = 12 + b2
√(22 − 12) = √b2
√3 = b = adjacent length h
Trigonometric Functions Secant, Cosecant and Cotangent:
The acute angle secant, cosecant and cotangent trig functions are ratios defined in terms of the cosine, sine, and tangent:
Cosecant A = c / a
Hypotenuse / Opposite = 1 / sine A
Secant A = c / b
Hypotenuse / Adjacent = 1 / cosine A
Cotangent A = b / a
Adjacent / Opposite = 1 / tangent A
… and cosecant, secant and cotangent are abbreviated as csc, sec and cot:
csc 30° = 1 / sin 30° = 1 / (1 / 2) = 2
sec 45° = 1 / cos 45° = 1 / (√2 / 2) = √2
cot 60° = 1 / tan 60° = 1 / √3 = √3 / 3
Cosecant means compliments secant and cotangent means compliments tangent:
sec A = csc (90° − A) and csc A = sec (90° − A)
tan A = cot (90° − A) and cot A = tan (90° − A)
By knowing the values of any one acute angle trigonometric function; the other five function values can be found by the Pythagorean Theorem to obtain length of an unknown triangle side and then by definition for each trig function.
Copyright © DigitMath.com
All Rights Reserved.
| Addition |
| Subtraction |
| Multiplication |
| Division |
| Prime Numbers |
| Decimals and Place Value |
| Square Root |
| Rational and Irrational Numbers |
| Multiplication Table |
| Adding Decimals |
| Subtracting Decimals |
| Multiplying Decimals |
| Square Numbers Conversion Tables |
| Adding Fractions |
| Subtracting Fractions |
| Multiplying Fractions |
| Dividing Fractions |
| Fractions to Decimals |
| Fraction to Percent |
| Factoring Polynomials |
| Factors and Factoring Defined |
| Prime Factorization |
| Algebraic Expressions and Math Terms |
| Important Algebraic Expressions |
| Difference of Squares |
| Factoring Trinomials |
| Factoring by Grouping |
| Cube-Formula(s) |
| Graphing Linear Equations |
| Linear Equations In Two Variables |
| System of Equations |
| Linear Function |
| Distance Formula |
| Midpoint Formula |
| Absolute Value |
| Polynomial Long Division |
| Synthetic Division |
| Radicals Adding Subtracting |
| Radical Expressions |
| Simplifying Radical Expressions |
| Factoring Quadratic Equations |
| Factoring by Completing the Square |
| Quadratic Equation Formula |
| Common Logarithm Tables |
| Logarithms Definition |
| Logarithm Properties |
| Common Logarithms |
| Antilogs |
| Natural Logarithms |
| Sequence Convergence & Divergence |
| Summation Notation |
| Factorials |
| Factorials for Binomial Expansion |
| Pascals Triangle |
| Mathematical Induction |
| What are Parallelograms? |
| Parallelogram Area |
| Perimeter of a Parallelogram |
| What is a Quadrilateral? |
| 3×3 Matrix Determinant |
| 4×4 Matrix Determinant |
| 3×3 Cramer’s Rule |
| Circle |
| Ellipse |
| Parabola |
| Hyperbola |
| Babylonian/Pythagorean/Egyptian |
| Greek Mathematics |
| Chinese Indian Islamic Math |
| Medieval European Renaissance Math |
| Scientific Revolution Math |
| Modern Math |
| Twentieth Century Math |
| Using Trigonometric Functions Table |